type
status
date
slug
summary
tags
category
icon
password
需熟练背诵翻译和推理规则！！
如果靠“理解意思”做翻译推理，就相当于做计算不被九九乘法表，见到 8×8
要一个一个做相加，慢且容易理解错。
一、题型特征
题干或选项中包含较多如：“如果…那么…”、“只有…才…”、“除非…否则…”、 “…或者…”、“有的…是…”、“所有…都…”等逻辑关联词
二、解题思路：先翻译，后推理
先把带有逻辑关联词的句子按翻译规则化成 A→B 的形式再根据推理规则进行推理
三、翻译规则（1-4 必考，必须熟练掌握；5 需了解）
1. 前推后（前半句 推 后半句）
- 如果/要是……那么/就……（那么/就 可省略）
- 只要……就……（就 可省略）
- 若……，则……
- 所有/凡是……都……
- ……就/都/则……
- 因为……所以……，……使得……，……有助于……
注：上面几个表示因果关系的关联词，如果选项不涉及句中内容，就不用翻；如果选项当中涉及到了这些句子的内容，按 前推后 翻译
例 1：如果你坚持运动，那么能减肥成功 运动 → 减肥
例 2：只要没有减肥成功，就说明没有坚持运动 —减肥 → —运动
2. 后推前（后半句 推 前半句）
- 只有……才……
- ……才……
- 除非……否则不……
- 不……不……
例1：只有你坚持运动，才能减肥成功 减肥 → 运动
例2：减肥不成功，才会坚持运动 运动 → —减肥
例3：除非没有减肥成功，否则没有坚持运动 运动 → —减肥
例4：不坚持运动，不能减肥成功 减肥 → 运动
3. 谁是必要条件谁在箭头后，另外半句放在箭头前
必要条件替换词：前提、必要假设、必不可少的、必须/必然／一定是
例1：坚持运动是减肥成功的必要条件 减肥 → 运动坚持运动是必要条件，故 运动 放在箭头后
例2：减肥不成功，不坚持运动是前提 —减肥 → —运动不坚持运动是前提，故 —运动 放在箭头后
例3：想减肥成功，必须坚持运动 减肥 → 运动必须的是 坚持运动，故 运动 放在箭头后
例4：不坚持运动，必然不会减肥成功 —运动 → —减肥必然的是 不会减肥成功，故 —减肥 放在箭头后
4. 否一推一（否前半句 推 后半句 或 否后半句 推 前半句）
- 除非……否则……
- ……，否则……
- ……，除非……
- ……或者……
- 或者……或者……
- ……和……至少有一个
例 1：除非没有减肥成功，否则没有坚持运动
—（—减肥） → —运动； —（—运动） → —减肥
例 2：不能减肥成功，除非坚持运动
—（—减肥） → 运动； —运动 → —减肥
例 3：坚持运动 或者 减肥不成功
—运动 → —减肥； —（—减肥） → 运动
例４：坚持运动和减肥成功至少有一个为真
—运动 → 减肥； —减肥 → 运动
一个特例：若要人不知，除非己莫为 翻译为：人不知→己不为，己为→人知若和除非混用，是非常特殊的句子，不作为重点。
5. —(A 且B)可翻译为：一推否一（一个成立 推 另一个不成立）
原理：—（A 且 B）= —A 或 —B = A→—B = B→—A
- A 和 B 不能共存
- 不可能同时出现 A 和 B
- 做 A 和做 B 的 不是同一批人
例 1：减肥成功和不坚持运动不会同时成立 —（减肥且—运动）
减肥 → —（—运动）； —运动 → —减肥
例 2：不可能既不坚持运动又不减肥成功 —（—运动且—减肥）
—运动 → —（—减肥）； —减肥→ —（—运动）
例 3：不坚持运动和减肥成功的不是同一批人 —（—运动且减肥）
—运动 → —减肥； 减肥 → —（—运动）
四、推理规则
1. 逆否等价：A→B＝—B→－A（必考，必须熟练掌握）
例：如果你减肥成功，那么你坚持运动 减肥→运动
＝只要你不坚持运动，就不会减肥成功 —运动→—减肥
＝所有减肥成功的都会坚持运动 减肥→运动
＝只有你坚持运动才能减肥成功 减肥→运动
＝除非你坚持运动，否则不会减肥成功 减肥→运动
＝除非减肥不成功，否则坚持运动 —运动→—减肥，－（－）减肥→运动
＝不会减肥成功，除非坚持运动 —运动→—减肥，－（－）减肥→运动
＝坚持运动，或者不会减肥成功 —运动→—减肥，－（－）减肥→运动
＝坚持运动和减肥不成功至少满足一个—运动→—减肥，－（－）减肥→运动
＝不坚持运动和减肥成功不能共存 —运动→—减肥，－（－）减肥→运动
＝坚持运动是减肥成功的必要条件 减肥→运动
＝减肥成功，坚持运动是前提 减肥→运动
＝减肥成功，必须坚持运动 减肥→运动
箭头前为真，推出箭头后必为真； 箭头后为假，推出箭头前必为假；
注意：箭头前为假、箭头后为真，只能推出可能性结论，不能推出确定结论。
例 1：如果你减肥成功，那么你坚持运动。 减肥→运动
已知：减肥成功，则：一定坚持运动
已知：没有坚持运动，则：一定没有减肥成功
已知：没有减肥成功，则：可能坚持运动，也可能不坚持运动
已知：坚持运动，则：可能减肥成功，也可能不减肥成功
例 2：或者没有坚持运动，或者没有减肥成功。 减肥→—运动
已知：减肥成功，则：一定没有坚持运动
已知：坚持运动，则：一定没有减肥成功
已知：没有减肥成功，则：可能坚持运动，也可能不坚持运动
已知：没有坚持运动，则：可能减肥成功，也可能减肥不成功
2. 鲁滨逊定律：A→B＝—A 或 B（了解即可）
原理：—A 或 B 的翻译是 —（—A）→B，即Ａ→B
3. 传递律：A→B 且 B→C，可得：A→C（必考，必须熟练掌握）
例：如果你减肥成功，那么你坚持运动。只有意志坚强，才能坚持运动。
句 1：减肥→运动，句 2：运动→坚强，故：减肥→坚强
由此可知，以下论断均成立：
只要减肥成功，说明意志坚强
只有减肥不成功，才会意志不坚强或者意志坚强，或者减肥不成功
减肥成功和意志不坚强不会同时成立
4. 且 与 或（几乎必考，必须熟练掌握）
①且 的替换词：和／与/同时、既…又…、不仅…而且…、虽然…但是…
注意：虽然 A 但是 B，意思上是转折关系，但逻辑上表示 A 且 B 同时成立
例 1：小红虽然不爱运动，但是不胖。翻译为：小红不爱运动 且 小红不胖
②A 为真 且 B 为真→A 且 B 为真
③A 且 B→A ； A 且 B→B
例 2：已知 小红又聪明又美丽，则：小红美丽 为真，小红聪明 为真
④或 的涵义：至少有一个（A 或 B 为真＝A 和 B 至少有一个为真）
⑤A→A 或 B ； B→A 或 B ； A 且 B→A 或 B
例 3：已知 张三去参加活动。则：张三或李四去参加活动 为真
已知 李四去参加活动。则：张三或李四去参加活动 为真
已知 张三和李四都去参加活动。则：张三或李四去参加活动 为真
⑥A 或 B 为真，推不出确定结论，A 可能为真可能为假；B 可能为真可能为假
例 4：已知 张三或李四去参加活动。那么张三去参加活动了吗？
结论：张三可能去，也可能不去，不能得到确定结论
⑦A 或 B 为真，可得：－A→B，－B→A
例 5：张三或李四去参加活动。
已知：张三没去，可得：李四一定去。
已知：李四没去，可得：张三一定去。
已知：张三去了，不能推出 李四是否一定去，李四可能去也可能不去
例 6：张三没去参加活动 或 李四没去参加活动。
已知：张三去了，可得：李四一定没去。
已知：李四去了，可得：张三一定没去。
已知：李四没去，不能推出 张三是否一定去，张三可能去也可能不去
⑧德摩根定理：－（A 且 B）＝－A 或-B ；－（A 或 B）＝－A 且-B
例 7：已知 并非张三或李四去参加活动。 则：张三没去 并且 李四没去
例 8：已知 张三和李四不会一起参加活动。则：张三没去 或者 李四没去
⑨－（A→B）＝A 且—B
原理：—（A→B）＝－（—A 或 B）＝－（－A）且—B＝A 且—B
⑩要么 A 要么 B：A 和 B 二选一。不能同时成立，不能同时不成立
例 9：要么张三参加活动，要么李四参加活动。
已知：张三去，可得：李四一定不去。
已知：李四没去，可得：张三一定去。
5. 所有 与 有的（部分省考考频高，冲刺行测 80 分必会）
①所有 A 是 B：A→B，－B→－A ；所有 A 不是 B ：A→－B，B→－A
②有的 的涵义：至少有一个(1≤有的≤所有)
③有的 A 是 B 翻译为：有的 A→B
注意：有的 A→B 不能推出 有的－B→－A “有的”不能应用“逆否等价”
例 1：有的人爱美 不能推出 有的不爱美的不是人
④已知：有的 A→B，B→C，可得：有的 A→C
例 2：有的人爱美，只要爱美一定聪明
句 1：有的人→爱美，句 2：爱美→聪明 故可得：有的人→聪明，即有的人聪明
注意：两个“有的”命题不能应用“传递律”
例 3：有的人爱美，有的爱美的人是聪明人
有的人→爱美，有的爱美→聪明 不能推出 有的人聪明
⑤所有 A 是 B →有的 A 是 B； 某一个 A 是 B →有的 A 是 B
注意：不能反推
例 4：所有人都爱美 推出 有的人爱美；有的人爱美 不能推出 所有人爱美
例 5：小红爱美 推出 有的人爱美；有的人爱美 不能推出 小红爱美
⑥有的 A 是 B ＝ 有的 B 是 A
例 6：有些爱美的人聪明 ＝ 有些聪明的人爱美
注意：有的 A 是 B 不能推出 有的 A 不是 B；
有的 A 不是 B 不能推出 有的 A 是 B
原理：有的 A 是 B 包含一种特殊情况：所有 A 都是 B，此时不满足有的 A 不是 B例 7：有的人考试及格 不能推出 有的人考试不及格
⑦有的 A 不是 B ＝ 有的不是 B 的是 A
注意：有的 A 不是 B 不能推出 有的 B 不是 A
例 8：有些爱美的人不聪明 ＝ 有些不聪明的人爱美
例 9：有些爱美的人不聪明不能推出有些聪明的人不爱美（如下图）
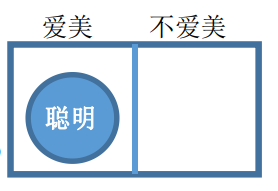
6. 二难推理（考频较低，冲刺行测 80 分必会）
①A→B 且－A→B ，可得：B
例 1：有山必有树，无山必有树
句 1： 山→树；
句 2：—山→树故一定有树。
例 2：有山必有树，有山必无树
句 1：山→树 = —树→—山
句 2：山→—树 = 树→—山
故一定无山。
②A 或 B 为真 且 A→C 且 B→C ，可得：C
例 3：山上有树或者有花。若有树则下雨，若有花则下雨。
句 1：有树或有花 为真
句 2：有树→下雨
句 3：有花→下雨
故：一定会下雨。
例 4：山上无树或者无花。若下雨则有树，若下雨则有花。
句 1：—有树 或 —有花 为真
句 2：下雨→有树= —有树 → —下雨
句 3：下雨→有花= —有花 → —下雨
故：一定不会下雨。
③A 或 B 为真 且 A→C 且 B→D ，可得：C 或 D
例 5：山上有树或者有花。若有花则下雨，若有树则刮风。
句 1：有树或有花 为真
句 2：有花→下雨
句 3：有树→刮风
故：一定会下雨或刮风
例 6：山上无树或者无花。若下雨则有花，若刮风则有树。
句 1：—有树 或 —有花 为真
句 2：下雨→有花= —有花 → —下雨
句 3：刮风→有树= —有树 → —刮风
故：一定不会下雨或者不会刮风
一定不会既刮风又下雨
- 作者:Herman
- 链接:https://note.xinfaye.top/article/b2792a86-8c11-482f-9db8-53e6e7218656
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。
